Path testing is an approach to testing where you ensure that every path through a program has been executed at least once. You normally use a dynamic analyzer tool or test coverage analyser to check that all of the code in a program has been executed. However, testing all paths does not mean that you will find all bugs in a program. Many bugs arise because programmers have forgotten to include some processing in their code, so there are no paths to execute. Some bugs are also related to the order in which code segments are executed. For example, if segments a, b and c are executed <a, b, c>, then the program may work properly. However, if they are executed <a, c, b> then an error may arise. It is practically impossible to test all orders of processing as well as all program paths.
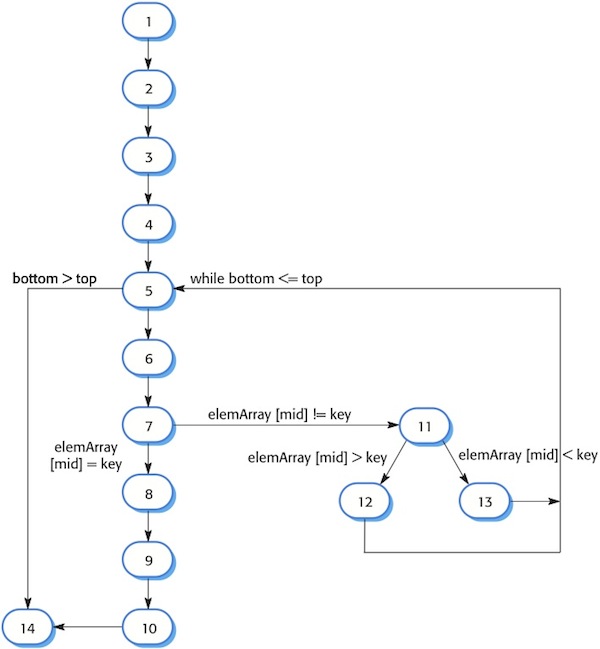
The starting point for path testing is a program flow graph. This is a skeletal model of all paths through the program. A flow graph consists of nodes representing decisions and edges showing flow of control. The flow graph is constructed by replacing program control statements by equivalent diagrams. If there are no goto statements in a program, it is a simple process to derive its flow graph. Each branch in a conditional statement (if-then-else or case) is shown as a separate path. An arrow looping back to the condition node denotes a loop. I have drawn the flow graph for a binary search method in Figure 1. To make the correspondence between this and binary search routine more obvious, I have shown each statement as a separate node where the node number corresponds to the line number in the program.
The objective of path testing is to ensure that each independent path through the program is executed at least once. An independent program path is one that traverses at least one new edge in the flow graph. In program terms, this means exercising one or more new conditions. Both the true and false branches of all conditions must be executed.
Each node in a flow graph represents a line in the program with an executable statement. By tracing the flow, therefore, you can see that the independent paths through the binary search flow graph are:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 14
1, 2, 3, 4, 5, 14
1, 2, 3, 4, 5, 6, 7, 11, 12, 5, …
1, 2, 3, 4, 6, 7, 2, 11, 13, 5, …
If all of these paths are executed we can be sure that every statement in the method has been executed at least once and that every branch has been exercised for true and false conditions. The number of tests that you need to ensure that all paths through the program are exercised is the same as the cyclomatic complexity of the code fragment that is being tested.

Figure 1: Flow graph for a binary search routine
R.L. Glass (2008). Two Mistakes and Error-Free Software. IEEE Software. 25 (4), 95–96.